Le noyau de l'appli linéaire c'est la plus "belle" solution mais peut-être qu'il n'a pas vu les appplis linéaires.
Dans le cas général il faut voir que, si l'on se place dans le Rev R^n, l'ensemble des vecteurs u=(x1, x2, ..., x_n ) qui vérifient:
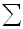 (de i=1 à n) des a_i x_i=0 est un sev de R^n (ça se voit très facilement).
(de i=1 à n) des a_i x_i=0 est un sev de R^n (ça se voit très facilement).
Ici on a trois équations de ce type, donc l'ensemeble considéré est l'intersection de trois sev de R^4 donc c'est un sev de R^4
Citation :
 le deuxieme semestre s'annonce mal, j'aime pas l'analyse et l'algebre... le deuxieme semestre s'annonce mal, j'aime pas l'analyse et l'algebre...
|
L'algèbre linéaire c'est super tu verras, fais un effort... 
Message édité par Profil supprimé le 12-03-2006 à 20:23:24

 FORUM HardWare.fr
FORUM HardWare.fr

 Emploi & Etudes
Emploi & Etudes

 Aide aux devoirs
Aide aux devoirs

 [L1] Incompréhension sur un exo d'algèbre linéaire
[L1] Incompréhension sur un exo d'algèbre linéaire FORUM HardWare.fr
FORUM HardWare.fr

 Emploi & Etudes
Emploi & Etudes

 Aide aux devoirs
Aide aux devoirs

 [L1] Incompréhension sur un exo d'algèbre linéaire
[L1] Incompréhension sur un exo d'algèbre linéaire